회귀 분석
Scikit-learn
1. 사이킷럿 모듈 설치
- pip install scikit-learn
2. 내장된 예제 데이터
- 사이킷런에는 별도의 외부 웹사이트에서 데이터 세트를 다운로드 받을 필요없이 예제로 활용할 수 있는 간단하면서도 좋은 데이터 세트가 내장되어 있다. 이 데이터는 datasets 모듈에 있는 여러 API를 호출해 만들 수 있다.
<분류나 회귀 연습용 예제 데이터>
| API명 | 설명 |
|---|---|
| datasets.load_digits() | 분류용, 0에서 9까지 숫자 이미지 픽셀 데이터셋 |
| datasets.load_iris() | 분류용, 붓꽃에 대한 피처를 가진 데이터셋 |
| datasets.load_breast_cancer() | 분류용, 위스콘신 유방암 피처들과 악성/음성 레이블 |
| datasets.load_boston() | 회귀용, 미국 보스톤 집 피처들과 가격 데이터셋 |
| datasets.load_diabetes() | 회귀용, 당뇨 데이터셋 |
회귀분석
머신러닝(Machine Learning)은 인공지능의 한 분야로 기계 스스로 대량의 데이터로부터 지식이나 패턴을 찾아 학습하고 예측하는 알고리즘 기법을 통칭한다
예측 알고리즘
| Types | Tasks | Algorithms |
|---|---|---|
| 지도 학습 (Supervised Learning) |
예측 (Prediction) |
Linear Regression SVM : Support Vector Machine Random Forest KNN : K Nearest Neighbor |
1. 회귀 분석 분류
1) 독립변수의 개수로 분류
단순 회귀 분석(Simple Linear Regression)
- 독립변수가 1개인 회귀 분석 방법
y = ax + b # a : 회귀계수(기울기), b : 절편, x : 독립변수
- 독립변수가 1개인 회귀 분석 방법
다중 회귀 분석(Mulple Linear Regression)
- 독립변수가 2개 이상인 회귀 분석 방법
y = ax1 + bx2 + cx3 + d # 독립변수 : x1, x2, x3
- 독립변수가 2개 이상인 회귀 분석 방법
2) 단순 회귀 분석
- 일반적으로 소득이 증가하면 소비가 증가하는 것처럼, 어떤 변수 (독립변수 X)가 다른변수(종속변수 Y)에 영향을 준다면 두 변수 사이에 선형 관계가 있다고 말한다. 이와 같은 선형관계를 알고 있다면 새로운 독립변수 X값이 주어졌을 때 거기에 대응하는 종속변수 Y값을 예측할 수 있다.
- 이처럼 두 변수 사이에 일대일로 대응되는 확률적, 통계적 상관성을 찾는 알고리즘을 단순회귀분석(Simple Linear Regression)이라고 말한다.
- 단순회귀분석을 대표적인 지도학습의 유형이다.
수학적으로 종속 변수 Y와 독립 변수 X 사이의 관계를 1차함수 Y = aX + b로 나타낸다. 단순회귀분석 알고리즘은 훈련 데이터를 이용하여 직선의 기울기(a)와 직선이 y축과 교차하는 지점인 y절편(b)을 반복 학습을 통해서 찾는다.
일차 방정식의 계수 a(기울기)와 b(절편)를 찾는 과정이 단순회귀분석 알고리즘이다.
2. 최소 제곱법(Method of Least Squares)
실제값과 예측값 차이 에 대한 제곱의 합을 최소로 해서 f(x)를 구하는 방법
- N회 측정핚 측정값 y1, y2,….,yn이 어떤 다른 측정값 x1, x2,…,xn의 함수라고 추정할 수 있을때, 측정값 y와 함수값 f(x)의 차이를 제곱핚 것의 합
이 최소가 되도록 하는 함수 f(x)를 구하는 것이 최소 제곱법의 원리이다.
scikit-learn 에서 최소 제곱법 구현 방법
linear_model . LinearRegression()
1) 실습
y = ax + b 처럼 데이터를 만들어 회귀문제를 풀어 보자.
여기서는 y = 3x – 2 인 경우에 최소 제곱법으로 기울기와 절편을 구해보자
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# 학습 데이터 생성
x = np.random.rand(100, 1) # 0~1까지 난수 100개 만들기
print(x)
# %%
# 회귀식 생성
x = x * 4 - 2 # 값의 범위 : -2 ~ 2 (min 0, max 1)
y = 3 * x - 2 # y = 3x - 2 (x의 독립변수로 인해서 y값이 결정됨)
# 모델생성 : 최소 제곱법으로 구현
model = linear_model.LinearRegression()
# 학습
model.fit(x, y)
# 계수 (기울기) , 절편
print('기울기(회귀계수):', model.coef_)
print('절편:', model.intercept_)
# %%
# 산점도 그래프 출력
plt.scatter(x, y, marker='+')
plt.show()
# 오차가 없는 y = 3x-2 예측결과 그래프
# y = ax + b 에서, 기울기 a =3, 절편 b = -2가 구해졌음.
2) 실습
- y = ax + b 처럼 데이터를 만들어 회귀문제를 풀어 보자.
- 여기서는 y = 3x – 2에 정규분포 난수를 더했을때, 최소 제곱법으로 기울기와 절편을 예측해 보자
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# 학습 데이터 생성
x = np.random.rand(100, 1) # 0~1까지 난수를 100개 생성
print(x)
# %%
x = x * 4 - 2 # 값의 범위 -2 ~ 2
y = 3 * x - 2 # y = 3x – 2
# 표준 정규 분포(평균 0, 표준 편차 1)의 난수를 추가함
y += np.random.randn(100, 1)
print(y)
# %%
# 모델 생성 : 최소 제곱법으로 구현
model = linear_model.LinearRegression()
# 모델 학습
model.fit(x, y)
# 예측값 출력
print(model.predict(x))
# %%
# 계수, 절편 확인
print('계수(기울기):', model.coef_)
print('절편:', model.intercept_)
# %%
# 산점도 그래프 출력
plt.scatter(x, y, marker='+') # 실제 데이터 +
plt.scatter(x, model.predict(x), marker='o') # 예측값 o
plt.show()
# 오차가 있는 y = 3x – 2 예측결과 그래프
결정계수 (𝐑𝟐)
- 회귀 결과의 타당성을 객관적으로 평가하는 지표로 결정계수를 사용핚다.
- 결정계수의 값이 1에 가까우면 성능이 좋은 예측 모델이라고 할수 수 있다.
- scikit-learn 에서 결정계수는 model.score() 함수로 구할 수 있다.

- 결정계수가 0 에 가까울 수록 예측 성능이 좋지 않고, 1 에 가까울 수록 예측 성능이 좋다고 할 수 있다.
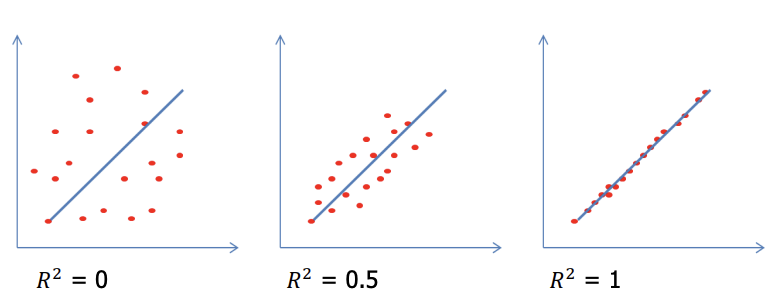
1. 단순회귀분석 - 결정계수
1) 실습
- y = ax + b 처럼 데이터를 만들어 회귀문제를 풀어 보자.
- 여기서는 y = 3x – 2에 정규분포 난수를 더했을때, 최소 제곱법으로 기울기와 절편을 예측해 보자.
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# %%
# 학습 데이터 생성
x=np.random.rand(100, 1) # 0~1 까지 난수 100개
x = x * 4 - 2 # x는 -2~2 까지 나옴. x의 최소는0 최대는1
y = 3 * x - 2
# 표준 정규 분포(평균0, 표준편차1)의 난수를 추가
y += np.random.randn(100, 1)
# %%
# 모델 : 최소 제곱법
model = linear_model.LinearRegression()
# 학습
model.fit(x, y)
# %%
# 계수, 절편, 결정 계수
print('계수:', model.coef_)
print('절편:', model.intercept_)
r2 = model.score(x, y)
print('결정계수:', r2)
# %%
# 산점도 그래프 출력
plt.scatter(x, y, marker ='+')
plt.scatter(x, model.predict(x), marker='o')
plt.show()
2. 다항회귀 분석
- 2차 방정식
1) 실습
- y = ax^2 + b 형태의 데이터를 만들어 회귀문제를 풀어 보자.
- 여기서는 y = 3x^2 – 2에 정규분포 난수를 더했을때, 최소 제곱법으로 기울기와 절편을 예측해 보자.
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# %%
# 학습 데이터 생성
x = np.random.rand(100, 1) # 0 ~ 1 까지 난수 100개 생성
x = x * 4 - 2 # x의 범위는 -2 ~ 2
y = 3 * x**2 - 2 # y = 3x^ - 2
y += np.random.randn(100, 1) # 표준 정규 분포(평균 0, 표준편차1)의 난수 추가
# %%
# 모델 선정
model = linear_model.LinearRegression()
# 학습
model.fit(x**2, y) # x 제곱
# %%
print('계수:', model.coef_)
print('절편:', model.intercept_)
print('결정계수:', model.score(x**2, y)) # x 제곱
# %%
plt.scatter(x, y, marker='+')
plt.scatter(x, model.predict(x**2), marker='o')
plt.show()
3. 다중 선형회귀 분석
1) 실습
- y = ax1 + bx2 + c 형태의 데이터를 만들어 회귀문제를 풀어 보자.
- 여기서는 y = 3x1 – 2x2 + 1 에 정규분포 난수를 더했을때, 최소 제곱법으로 회귀계수와 절편을 예측해 보자.
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
# %%
# 독립 변수가 2개로 설정
# 학습데이터 생성
# x_1, x_2 동일한 형태로 -2~2 의 범위로 난수 100개 생성
x1 = np.random.rand(100, 1)
x1 = x1 * 4 - 2
x2 = np.random.rand(100,1)
x2 = x2 * 4 - 2
y = 3 * x1 - 2 * x2 + 1
y += np.random.randn(100, 1) # 표준 정규 분포(평균0, 표준편차1) 의 난수 추가
# %%
# x1, x2 값을 가진 행렬 생성 (2차원배열)
x1_x2 = np.c_[x1, x2]
print(x1_x2)
# %%
# 모델 생성
model = linear_model.LinearRegression()
# 학습
model.fit(x1_x2, y)
# %%
print('계수:', model.coef_)
# y의 설정된 계수 3과, -2의 비슷한 수치가 나옴
print('절편:', model.intercept_)
print('결정계수:', model.score(x1_x2, y))
# 결정계수 1에 근접하는 0.93 정도로 성능이 좋다고 볼수있다.
# %%
# 산점도 그래프
y_ = model.predict(x1_x2)
plt.subplot(1,2,1) # 1행 2열의 첫번째 그래프
plt.scatter(x1, y, marker='+') # 실제 데이터
plt.scatter(x1, y_, marker='o') # 예측 데이터
plt.xlabel('x1')
plt.ylabel('y')
plt.subplot(1,2,2)
plt.scatter(x2, y, marker='+')
plt.scatter(x2, y_, marker='o')
plt.xlabel('x2')
plt.ylabel('y')
plt.tight_layout()
plt.show()
4. 보스턴 주택 가격 회귀 분석
- LinearRegression을 이용핚 보스턴 주택 가격 회귀분석
- LinearRegression 클래스를 이용핚 선형회귀 모델을 만들어 보자.
lr = LinearRegression()
- 사이킷런에 내장된 데이터셋인 보스턴 주택가격 데이터를 이용한다.
boston = datasets.load_boston()
보스턴 집값 데이터 : 인덱스 506행, 컬럼:14열
14개의 컬럼 정보
| 순서 | 컬럼 | 내용 |
|---|---|---|
| 0 | CRIM | 인구 1인당 범죄 발생 수 |
| 1 | ZN | 25,000평방 피트 이상의 주거 구역 비중 |
| 2 | INDUS | 소매업 외 상업이 차지하는 면적 비율 |
| 3 | CHAR | 찰스강 위치 변수 (1:강 주변, 0:이외) |
| 4 | NOX | 일산화 질소 농도 |
| 5 | RM | 집의 평균 방 수 |
| 6 | AGE | 1940년 이전에 지어짂 비율 |
| 7 | DIS | 5가지 보스턴시 고용 시설까지의 거리 |
| 8 | RAD | 순환 고속도로의 접근 용이성 |
| 9 | TAX | $10,000당 부동산 세율 총계 |
| 10 | PTRATIO | 지역별 학생과 교사 비율 |
| 11 | B | 지역별 흑인 비율 |
| 12 | LSTAT | 급여가 낮은 직업에 종사하는 인구 비율(%) |
| 13 | 주택 가격(단위 : $1,000) |
실습)
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_boston
# boston 데이셋 로드
boston = load_boston()
print(boston)
# %%
# boston DataFrame으로 변환
bostonDF = pd.DataFrame(boston.data, columns=boston.feature_names) # feasture_names이 있는 Data 불러오기
print(bostonDF.info())
print(bostonDF.head())
# %%
# boston 데이터셋의 target 열(컬럼)은 주택 가격
# boston.target 을 price 컬럼으로 추가함.
bostonDF['price'] = boston.target
print(bostonDF.head())
print(bostonDF.shape)
# 컬럼추가해서 파일로 내보내기
bostonDF.to_csv('boston.csv', encoding='utf-8')
# %%
# 다음의 각 컬럼 RM, ZN, INDUS, NOX, AGE, PTRATIO, LSTAT, RAD 의 총 8개의 컬럼에
# 대해서 값이 증가핛수록 PRICE에 어떤 영향을 미치는지 분석하고 시각화를 해보자
# %%
# 2행 4열 그래프 생성
fig, axs = plt.subplots(figsize=(16,8), nrows=2, ncols=4)
im_features = ['RM', 'ZN', 'INDUS', 'NOX', 'AGE', 'PTRATIO', 'LSTAT', 'RAD']
for i, feature in enumerate(im_features) :
row = int(i / 4)
col = i % 4
sns.regplot(x=feature, y='price',
data=bostonDF,
ax=axs[row][col]) # 그래프 위치
plt.show()
# * RM(방개수)와 LSTAT(하위 계층의 비율)이 PRICE에 영향도가 가장 두드러지게 나타남.
# 1. RM(방개수)은 양 방향의 선형성(Positive Linearity)이 가장 크다.
# 방의 개수가 많을수록 가격이 증가하는 모습을 확연히 보여준다.
# 2. LSTAT(하위 계층의 비율)는 음 방향의 선형성(Negative Linearity)이 가장 크다.
# 하위 계층의 비율이 낮을수록 PRICE 가 증가하는 모습을 확연히 보여준다.
# train_test_split()을 이용해 학습과 테스트 데이터셋을 분리해서 학습과 예측을 수행한다.
# LinearRegression 클래스를 이용해서 보스턴 주택 가격의 회귀 모델을 만들어 보자
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# 모델평가 - r2_score 함수로 회귀계수를 구할수 있음.
from sklearn.metrics import mean_squared_error, r2_score
# %%
# train data와 test data를 분리하기 위해서 y 축을 분리 시킴
y_target = bostonDF['price']
# 'price' 컬럼을 삭제 하고 받아온 데이터를 리턴함.
x_target = bostonDF.drop(['price'], axis=1, inplace=False)
print(y_target.head())
print(x_target.head())
# %%
# 7:3 비율로 분리
# 교차 검증을 하기위해서 train data와 test data로 분할 해서 7:3 비율로 검증 진행
# overfitting 을 줄이기 위한 작업
x_train, x_test, y_train, y_test = train_test_split(x_target, # 13개의 컬럼 데이터
y_target, # price 컬럼 데이터
test_size=0.3, # 테스트 데이터의 비율 설정 0.3
random_state=156) # 난수의 시드를 임의 값으로 고정
# 분리된 데이터 확인
print(x_train)
print(y_train)
# %%
# 선형 회귀 수행
# 모델 생성
model = LinearRegression()
# 모델 학습
model.fit(x_train, y_train)
# 실제값은 y_test 임.
# 모델 예측 값 - 30% 비율이 데이터로 예측 결과
y_predict = model.predict(x_test)
print(y_predict)
# %%
# 모델 평가 - r2_scroe(실제데이터, 예측데이터)
print('결정계수:', r2_score(y_test, y_predict))
# 결정계수 0.75 정도면 성능이 높기는 하지만.. 애매하다
# 각 알고리즘 별로 학습능력 및 예측 능력이 달라진다.
# %%
# LinearRegression 으로 생성한 주택가격 모델의 회귀계수(coefficients)와 절편(intercept)을 구해보자
# 회귀계수는 LinearRegression 객체의 coef_ 속성으로 구할 수 있고,
# 절편은 LinearRegression 객체의 intercept_ 속성으로 구할 수 있다.
print('회귀계수값:', np.round(model.coef_, 1 )) # 소수 첫째자리
print('절편값:', model.intercept_)
# 회귀계수를 큰 값 순으로 정렬하기 위해서 Series로 생성함.
coff = pd.Series(data=np.round(model.coef_, 1), index=x_target.columns)
print(coff.sort_values(ascending=False))
RM(방개수)와 LSTAT(하위 계층의 비율)이 PRICE에 영향도가 가장 두드러지게 나타남.
RM(방개수)은 양 방향의 선형성(Positive Linearity)이 가장 크다.
- 방의 개수가 많을수록 가격이 증가하는 모습을 확연히 보여준다.
LSTAT(하위 계층의 비율)는 음 방향의 선형성(Negative Linearity)이 가장 크다.
- 하위 계층의 비율이 낮을수록 PRICE 가 증가하는 모습을 확연히 보여준다
5. 단순회귀분석 실습
- UCI(University of California, Irvine) 자동차 연비 데이터셋으로 단순회귀분석을 해보자
https://archive.ics.uci.edu/ml/datasets.php
1) 데이터 준비
2) 데이터 탐색
3) 분석에 활용할 속성(feature 또는 variable) 선택 및 그래프 그리기
- 독립변수 : weight(중량), 종속변수 : mpg(연비)
4) 훈련 데이터 / 검증 데이터 분할
- 앞에서 그린 산점도에서 ‘mpg’ 열과 선형관계를 보이는 ‘weight’ 열을 독립변수 x로 선택한다.
- 다음은 두 변수 간의 회귀 방정식을 구하기 위해서 훈련 데이터와 검증 데이터로 나눠서 모델을 구축한다.
- 다음 예제에서는 ‘weight’ 열을 독립 변수 x로 선택하고, 데이터를 7:3 으로 각각 분할한다.
- 훈련 데이터 274개, 검증 데이터 118개로 분할한다
5) 모델 학습 및 모델 검증
- sklearn 라이브러리를 이용하여 선형회귀분석 모델을 만든다.
- LinearRegression() 함수로 회귀분석 모델 객체를 생성한다.
- 생성된 모델을 이용하여 학습 데이터(train data)를 학습 시키기 위해서는 fit() 함수를 사용한다.
- 모델 객체에 fit() 함수를 적용하고 훈련 데이터(x_train, y_train)를 전달하면 모델이 학습을 통해 회귀 방정식의 계수 a(기울기), b(절편)를 찾는다.
- 학습을 마친 모델의 예측 능력을 평가하기 위해서 검증 데이터를 score() 함수에 전달하여 모델의 결정계수(R-제곱)를 구한다.
- 결정 계수의 값이 1에 가까우면 모델의 예측 능력이 좋다고 평가한다
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %%
# 1.데이터 준비
# csv 파일을 읽어와서 데이터프레임으로 변환
df = pd.read_csv('../data/auto-mpg.csv', header=None)
print(df)
# %%
# 컬럼명 설정
df.columns = ['mpg','cylinders','displacement','horsepower','weight','acceleration','model year','origin','name']
# %%
# 데이터 살펴보기
print(df.head())
# %%
# IPython 디스플레이 설정 - 출력할 열의 개수 늘리기
pd.set_option('display.max_columns', 10)
print(df.head())
# %%
# 2. 데이터 탐색
# %%
# 데이터 자료형 살펴 보기
df.info()
# %%
# 데이터 통계 요약정보 확인
print(df.describe())
# %%
# horsepower 열의 고유값 확인 : ['130.0' '165.0' '150.0' '140.0' ...]
print(df['horsepower'].unique())
# horsepower 열의 고유값 확인
# horsepower 열의 자료형 object(문자형)
# %%
# horsepower 열의 자료형 변경 (문자형 ->실수형)
df['horsepower'].replace('?', np.nan, inplace=True) # '?'을 np.nan으로 변경
df.dropna(subset=['horsepower'], axis=0, inplace=True) # 누락데이터 행을 삭제
df['horsepower'] = df['horsepower'].astype('float') # 문자형을 실수형으로 변홖
print(df.describe())
# 문자형에서 실수형으로 변환된 horsepower컬럼 출력됨
# %%
# 3. 분석에 활용할 속성(feature 또는 variable) 선택 및 그래프 그리기
# %%
# 분석에 활용한 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
print(ndf.head()) # 앞에서 5개의 데이터 출력
# %%
# 독립변수(x) weight(중량)와 종속 변수(y)인 mpg(연비) 간의 선형관계를 산점도 그래프로 확인
# 1.matplotlib으로 산점도 그리기
ndf.plot(kind='scatter', x='weight', y='mpg', c='coral', s=10, figsize=(10, 5))
plt.show()
# %%
# 2.seaborn으로 산점도 그리기
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1) # 1행 2열 첫번째 그래프
ax2 = fig.add_subplot(1, 2, 2) # 1행 2열 두번째 그래프
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax1, fit_reg=True) # 회귀선 표시
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax2, fit_reg=False) # 회귀선 미표시
plt.show()
# %%
# 3.seaborn 조인트 그래프 - 산점도, 히스토그램
sns.jointplot(x='weight', y='mpg', data=ndf) # 회귀선 없음
sns.jointplot(x='weight', y='mpg', kind='reg', data=ndf) # 회귀선 표시
plt.show()
# %%
# 4.seaborn pariplot으로 두 변수 간의 모든 경우의 수 그리기
sns.pairplot(ndf)
plt.show()
# %%
# 분석에 홗용핛 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
print(ndf.head())
# %%
# 독립변수(x) weight(중량)와 종속 변수(y)인 mpg(연비) 간의 선형관계를 산점도 그래프
# 1.matplotlib으로 산점도 그리기
ndf.plot(kind='scatter', x='weight', y='mpg', c='coral', s=10, figsize=(10, 5))
plt.show()
# weight(중량)이 적을수록 mpg(연비)가 높은 것을 알 수 있다.
# %%
# 2.seaborn으로 산점도 그리기
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1) # 1행 2열 첫번째 그래프
ax2 = fig.add_subplot(1, 2, 2) # 1행 2열 두번째 그래프
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax1, fit_reg=True) # 회귀선 표시
sns.regplot(x='weight', y='mpg', data=ndf, ax=ax2, fit_reg=False) # 회귀선 미표시
plt.show()
# %%
# 3.seaborn 조인트 그래프 - 산점도, 히스토그램
sns.jointplot(x='weight', y='mpg', data=ndf) # 회귀선 없음
sns.jointplot(x='weight', y='mpg', kind='reg', data=ndf) # 회귀선 표시
plt.show()
# %%
# 4.seaborn pariplot으로 두 변수 간의 모든 경우의 수 그리기
sns.pairplot(ndf)
plt.show()
# 같은 변수끼리 짝을 이루는 대각선 방향은 히스토그램을 그리고 서로 다른 변수간에는 산점도로 출력된다.
# %%
# 4. 훈련 데이터 / 검증 데이터 분할
# %%
# 앞에서 그린 산점도에서 ‘mpg’ 열과 선형관계를 보이는 ‘weight’ 열을 독립변수 x로 선택핚다.
# 다음은 두 변수 갂의 회귀 방정식을 구하기 위해서 훈련 데이터와 검증 데이터로 나눠서 모델을 구축한다.
# 다음 예제에서는 ‘weight’ 열을 독립 변수 x로 선택하고, 데이터를 7:3 으로 각각분할한다.
# 훈련 데이터 274개, 검증 데이터 118개로 분할한다.
# weight – 독립변수(x)
# mpg – 종속변수(y)
# %%
# 속성(변수) 선택
x=ndf[['weight']] # 독립 변수 : x
y=ndf['mpg'] # 종속 변수 : y
# train data 와 test data로 분할(7:3 비율)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, # 독립 변수
y, # 종속 변수
test_size=0.3, # 검증 30%
random_state=10) # 랜덤 추출 값
print('train data 개수: ', len(x_train))
print('test data 개수: ', len(x_test))
# %%
# 5. 모델 학습 및 모델 검증
# %%
# sklearn 라이브러리를 이용하여 선형회귀분석 모델을 만든다.
# LinearRegression() 함수로 회귀분석 모델 객체를 생성한다.
# 생성된 모델을 이용하여 학습 데이터(train data)를 학습 시키기 위해서는 fit() 함수를 사용한다.
# 모델 객체에 fit() 함수를 적용하고 훈련 데이터(x_train, y_train)를 전달하면 모델이 학습을 통해 회귀 방정식의 계수 a(기울기), b(절편)를 찾는다.
# 학습을 마친 모델의 예측 능력을 평가하기 위해서 검증 데이터를 score() 함수에 전달하여 모델의 결정계수(R-제곱)를 구한다.
# 결정 계수의 값이 1에 가까우면 모델의 예측 능력이 좋다고 평가한다
# %%
# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기
from sklearn.linear_model import LinearRegression
# 단순회귀분석 모델 객체 생성
lr = LinearRegression()
# train data를 가지고 모델 학습
lr.fit(x_train, y_train)
# 학습을 마친 모델에 test data를 적용하여 결정계수(R-제곱) 계산
r_square = lr.score(x_test, y_test)
print(r_square)
# %%
# 회귀식의 기울기
print('기울기 a: ', lr.coef_) # [-0.00775343]
# 회귀식의 y절편
print('y절편 b:', lr.intercept_) # 46.7103662572801
# 모델에 전체 x데이터를 입력하여 예측한 값 y_hat을 실제 값 y와 비교
y_hat = lr.predict(x) # 예측값 구함
plt.figure(figsize=(10, 5))
ax1 = sns.distplot(y, hist=False, label="y") # 실제 값
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1) # 예측한 값
plt.show()
- <모델이 예측한 값(y_hat)와 실제 값(y) 비교 결과>
- 출력된 결과를 보면 실제 값은 왼쪽으로 편향되어 있고, 예측값은 반대로 오른쪽으로 편중되는 경향을 보인다.
- 따라서 독립변수(weight)와 종속변수(mpg) 사이에 선형관계가 있지만, 모델의 오차를 더 줄일 필요가 있어 보인다.
6. 다항회귀분석
- UCI 자동차 연비 데이터셋으로 다항회귀분석을 해보자
1) 데이터 준비
2) 데이터 탐색
3) 분석에 활용할 속성(feature 또는 variable) 선택
- 독립변수 : weight(중량), 종속변수 : mpg(연비)
4) 훈련 데이터 / 검증 데이터 분핛
5) 모델 학습 및 모델 검증
- 단순회귀분석 결정계수 : 0.6822458558299325
- 다항회귀분석 결정계수 : 0.7087009262975481
- 단순회귀분석을 했을때 보다 다항회귀분석을 했을때 결정계수값이 높아진 것에서 알수 있듯이 직선보다 곡선으로 만들어진 회귀선이 데이터 패턴을 더욱 더 잘 설명핚다고 할 수 있다.
- train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력 : 곡선모양의 회귀선
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %%
# 1. 데이터 준비
# %%
# CSV 파일을 읽어와서 데이터프레임으로 변비비
df = pd.read_csv('../data/auto-mpg.csv', header=None)
# 열 이름 지정
df.columns = ['mpg','cylinders','displacement','horsepower','weight','acceleration','model year','origin','name']
# %%
# 2. 데이터 탐색
# %%
# horsepower 열의 자료형 변경 (문자형 ->실수형)
df['horsepower'].replace('?', np.nan, inplace=True) # '?'을 np.nan으로 변경
df.dropna(subset=['horsepower'], axis=0, inplace=True) # 누락데이터 행을 삭제
df['horsepower'] = df['horsepower'].astype('float') # 문자형을 실수형으로 변홖
print(df.describe()) # 데이터 통계 요약정보 확인
# %%
# 3. 분석에 활용할 속성(feature 또는 variable) 선택
# %%
# 분석에 활용할 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
# ndf 데이터를 train data 와 test data로 구분(7:3 비율)
x=ndf[['weight']] # 독립 변수 x
y=ndf['mpg'] # 종속 변수 y
# %%
# 4. 훈련 데이터 / 검증 데이터 분할
# %%
# train data 와 test data로 구분(7:3 비율)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=10)
print('훈련 데이터: ', x_train.shape) # 훈련 데이터: (274, 1)
print('검증 데이터: ', x_test.shape) # 검증 데이터: (118, 1)
# %%
# 5. 모델 학습 및 모델 검증
# %%
# sklearn 라이브러리에서 필요한 모듈 가져오기
from sklearn.linear_model import LinearRegression # 선형회귀분석
from sklearn.preprocessing import PolynomialFeatures # 다항식 변환
# 다항식 변환
poly = PolynomialFeatures(degree=2) # 2차항 적용
x_train_poly = poly.fit_transform(x_train) # x_train 데이터를 2차항으로 변환
print('원 데이터: ', x_train.shape) # 원 데이터: (274, 1)
print('2차항 변환 데이터: ', x_train_poly.shape) # 2차항 변환 데이터: (274, 3)
# x_train의 1개의 열이 x_train_poly 에서는 3개의 열로 늘어난
# %%
# train data를 가지고 모델 학습
model = LinearRegression() # 모델 만들기
model.fit(x_train_poly, y_train) # 모델 학습
# 학습을 마친 모델에 test data를 적용하여 결정계수(R-제곱) 계산
x_test_poly = poly.fit_transform(x_test) # x_test 데이터를 2차항으로 변환
r_square = model.score(x_test_poly, y_test) # 결정계수 구하기
print(r_square)
# 결정계수 : 0.7087009262975481
# %%
# train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력
y_hat_test = pr.predict(x_test_poly) # test data로 예측하기
fig = plt.figure(figsize=(10, 5)) # 그래프 크기 설정
ax = fig.add_subplot(1, 1, 1)
ax.plot(x_train, y_train, 'o', label='Train Data') # train data의 산점도
ax.plot(x_test, y_hat_test, 'r+', label='Predicted Value') # 모델이 학습핚 회귀선
ax.legend(loc='best') # 범례 설정
plt.xlabel('weight') # x축 라벨
plt.ylabel('mpg') # y축 라벨
plt.show()
# %% [markdown]
# * 단순회귀분석 결정계수 : 0.6822458558299325
# * 다항회귀분석 결정계수 : 0.7087009262975481
# * 단순회귀분석을 했을때 보다 다항회귀분석을 했을때 결정계수값이 높아진 것에서 알수 있듯이 직선보다 곡선으로 만들어진 회귀선이 데이터 패턴을 더욱 더 잘 설명한다고 할 수 있다.
# * train data의 산점도와 test data로 예측한 회귀선을 그래프로 출력 : 곡선모양의 회귀선
# %%
# 실제값 y와 예측값 y_hat 의 분포 차이 비교
# 모델에 전체 x데이터를 입력하여 예측한 값 y_hat을 실제 값 y와 비교
x_ploy = poly.fit_transform(x) # x 데이터를 2차항으로 변홖
y_hat = pr.predict(x_ploy) # 예측값 구하기
# displot() 함수 : 히스토그램 + 커널밀도함수
plt.figure(figsize=(10, 5)) # 그래프 크기 설정
ax1 = sns.distplot(y, hist=False, label="y") # 실제값
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1) # 예측값
plt.show()
# %% [markdown]
# * 단순회귀분석의 결과와 비교할 때 데이터가 어느 한쪽으로 편향되는 경향이 상당히 감소한 것을 알 수 있다.
# * 다항회귀분석이 더 적합한 모델이라고 볼 수 있다.
# * 실제값 y와 예측값 y_hat 의 분포 차이 비교
7. 다중회귀분석
- UCI 자동차 연비 데이터셋으로 다중회귀분석을 해보자
1) 데이터 준비
2) 데이터 탐색
3) 분석에 활용할 속성(feature 또는 variable) 선택
- 독립변수 : cylinders(실린더), horsepower(마력), weight(중량), 종속변수 : mpg(연비)
4) 훈련 데이터/ 검증 데이터 분할
5) 모델 학습 및 모델 검증
# To add a new cell, type '# %%'
# To add a new markdown cell, type '# %% [markdown]'
# %%
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# csv 파일을 읽어 와서 데이터프레임으로 변환
df = pd.read_csv('../data/auto-mpg.csv', header=None)
print(df)
# %%
# 열 이름 지정
df.columns = ['mpg','cylinders','displacement','horsepower','weight', 'acceleration','model year','origin','name']
print(df)
# %%
# 2. 데이터 검색
# %%
# horsepower 열의 자료형 변경 (문자형 -> 실수형)
df['horsepower'].replace('?', np.nan, inplace=True) # '?'을 np.nan으로 변경
df.dropna(subset=['horsepower'], axis=0, inplace=True) # 누락데이터 행을 삭제
df['horsepower'] = df['horsepower'].astype('float') # 문자형을 실수형으로 변환
print(df.describe())
# %%
# 3. 분석에 활용할 속성 선택
# 4. 훈련데이터 /검증 데이터 분할
# %%
# 분석에 활용한 열(속성)을 선택 (연비, 실린더, 출력, 중량)
ndf = df[['mpg', 'cylinders', 'horsepower', 'weight']]
# 독립변수와 종속변수 선택
x=ndf[['cylinders', 'horsepower', 'weight']] # 독립 변수 : cylinders, horsepower, weight
y=ndf['mpg'] # 종속 변수 : mpg
# train data 와 test data로 구분(7:3 비율)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=10)
print('훈련 데이터: ', x_train.shape) # 훈련 데이터: (274, 3)
print('검증 데이터: ', x_test.shape) # 검증 데이터: (118, 3)
# %%
# 5. 모델 학습 및 모델 검증
# %%
# sklearn 라이브러리에서 선형회귀분석 모듈 가져오기
from sklearn.linear_model import LinearRegression
# 단순회귀분석 모델 객체 생성
lr = LinearRegression() # 모델 만들기
# train data를 가지고 모델 학습
lr.fit(x_train, y_train) # 모델 학습
# 모델 평가
# 모델 학습이 완료된 다음에 검증데이터(x_test, y_test)를 사용하여 모델의 평가지표인
# 결정계수(R-제곱) 계산
r_square = lr.score(x_test, y_test)
print(r_square) # 결정계수 : 0.6939048496695599
# %%
# 회귀식의 기울기 : 독립변수 3개의 기욳기가 리스트로 리턴됨
print('X 변수의 계수 a: ', lr.coef_) # a : [-0.60691288 -0.03714088 -0.00522268]
# 회귀식의 y절편
print('상수항 b', lr.intercept_) # b : 46.414351269634025
# %%
# 모델이 예측한 값과 실제값을 비교
y_hat = lr.predict(x_test) # 예측값 구하기
print(y_hat)
plt.figure(figsize=(10, 5))
ax1 = sns.distplot(y_test, hist=False, label="y_test") # 실제값
ax2 = sns.distplot(y_hat, hist=False, label="y_hat", ax=ax1) # 예측값
plt.show()
- 다중회귀분석 결정계수 : 0.6939048496695599
- 다중회귀분석을 했을때 모델의 성능 지표인 결정계수값은 0.6939048496695599 으로 비교적 양호한 수준이다.
- 단순회귀분석의 결과와 비교할 때 데이터가 어는 한쪽으로 편향되는 경향은 그대로 남아 있지만 그래프의 첨도(뽀족한 정도)가 약간 누그러진 것을 볼 수 있다.